Wenn wir Bilder betrachten, empfinden wir besonders diejenigen als ästhetisch, deren Elemente einem bestimmten Verhältnis von Strecken und Flächen folgen. Diese Harmonielehre nennt sich der „Goldene Schnitt“ und findet viel Anwendung in der Natur.
Nun könnte man meinen: In Zeiten der durch künstliche Intelligenz gerenderten Grafiken, benötigen wir die vielen Grundlagen des Grafikdesigns nicht mehr. Das ist allerdings zu kurz gedacht, denn einerseits müssen wir aus den Vorschlägen der erstellten Bilder die beste Variante auswählen. Um hier gute Entscheidungen zu treffen, sind Kenntnisse über Proportionen und Ästhetik essenziell. Außerdem müssen wir unseren Wunsch auch klar formulieren können, damit wir ein optimales Ergebnis erzielen. Nur die Dinge die wir wirklich vollständig durchdringen können wir auch klar und unmissverständlich formulieren. Deswegen ist ganz besonders im Umgang mit generativer KI ein fundiertes Fachwissen unverzichtbar.
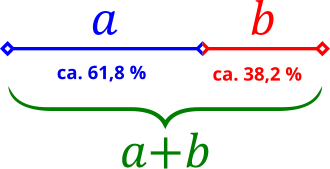
Geometrisch bedeutet der Goldene Schnitt, dass eine Strecke AB in zwei unterschiedlich lange Streckenabschnitte (a und b) geteilt wird. Setzt man nun a durch b gleich der Summe (a+b) / a, so erhält man φ mit dem Wert 1,618. Übrigens entspricht der exakte Wert von φ der Quadratwurzel aus 5 (√5). Die Streckenverhältnisse betragen ungefähr 3:2. Die nachfolgende Grafik verdeutlicht den Zusammenhang.
Um den „Goldenen Schnitt“ auf Flächen anzuwenden, ist es nicht notwendig, im Abitur den Mathematikleistungskurs erfolgreich abgeschlossen zu haben. Wir benötigen lediglich die Zahl φ. Wenn wir ein Rechteck mit einer Kantenlänge von einem Zentimeter haben und 1 * 1,618 multiplizieren, erhalten wir 1,618. Nun können wir ein Rechteck mit der Kantenlänge a = 1 und b = 1,618 zeichnen. Das hier entstandene Verhältnis ist die perfekte Harmonie und wird als „Goldener Schnitt“ bezeichnet.
Wenn wir in dieses Rechteck unser Quadrat mit der Kantenlänge von einem Zentimeter hineinlegen, erhalten wir eine rechteckige Fläche B, die sich nach dem gleichen Muster aufteilen lässt. Wenn wir diesen Vorgang nun ein paar Mal wiederholen, erhalten wir ein gekacheltes Muster. Tragen wir jetzt in jedes entstandene Quadrat einen Kreisbogen mit dem Radius der Kantenlänge ein, erhalten wir eine Spirale. Die Form aus Abbildung 2 dürfte den meisten bereits bekannt sein und nun wisst ihr auch, wie sie entsteht.

Die soeben beschriebene Spirale findet sich auch in der sogenannten Fibonacci Zahlenfolge wieder. Die Fibonacci Folge ist eine einfache rekursive Addition aus den beiden Vorgängern. Abbildung 3 zeigt, wie schnell sich die Fibonacci Folge berechnen lässt. Wir sehen, es ist dazu kein höheres Studium der Mathematik notwendig.
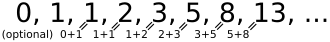

Wo finden wir den Goldenen Schnitt in der Anwendung? Neben Proportionen in Logos und anderen Grafiken nutzt man den Goldenen Schnitt oft in der Typografie. Die Höhenverhältnisse von kleinen zu großen Buchstaben folgen gern dem Abstand 1:1,618.
Ein typisches Szenario für die Anwendung des Goldenen Schnitts ist auch die Position von Objekten innerhalb einer Grafik. Um eine gute Illusion von Tiefe zu erzielen, benötigen die Objekte ein entsprechendes Verhältnis der Höhen zueinander. Aber auch der Bereich, wie Objekte im Abstand zueinander positioniert werden, lässt ein Bild ruhig und harmonisch oder aufgewühlt und unruhig wirken. Wir haben also zwei Möglichkeiten, durch den Goldenen Schnitt eine Stimmung beim Betrachter zu erzeugen. Durch gezielte Verletzung der Proportionen erreichen wir eine gewisse Unruhe, die durchaus ebenfalls gewünscht sein kann. Eine solche invertierte Strategie kann zum Beispiel in der Werbung eingesetzt werden, um sich aus der Masse abzuheben und so beim Betrachter Aufmerksamkeit zu erregen.



